Paper: Fair apportionment in the view of the Venice Commission’s recommendation

In most, though not all elections one can vote for candidates in electoral districts. Designing the districts is obviously a sensitive issue. How to do it well? Mathematical Social Sciences has just published our paper (joint with Péter Biró and Balázs Sziklai) on the Leximin apportionment method. The paper is free to download until 19 August 2015. 

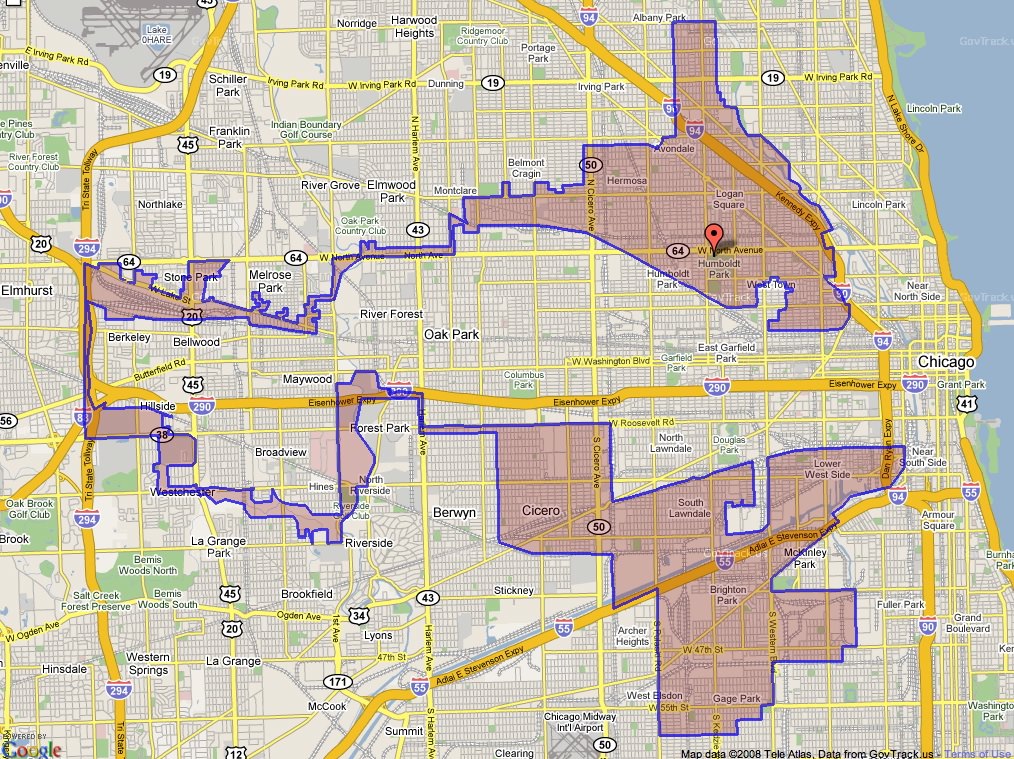When it comes to districting there are at least two issues. Gerrymandering refers to the arbitrary layout of districts to the legislators' benefit. It is sometimes difficult to tell what is OK, and what is manipulation, but there exist rather clear cases as the 4th district of Illinois on the right. 

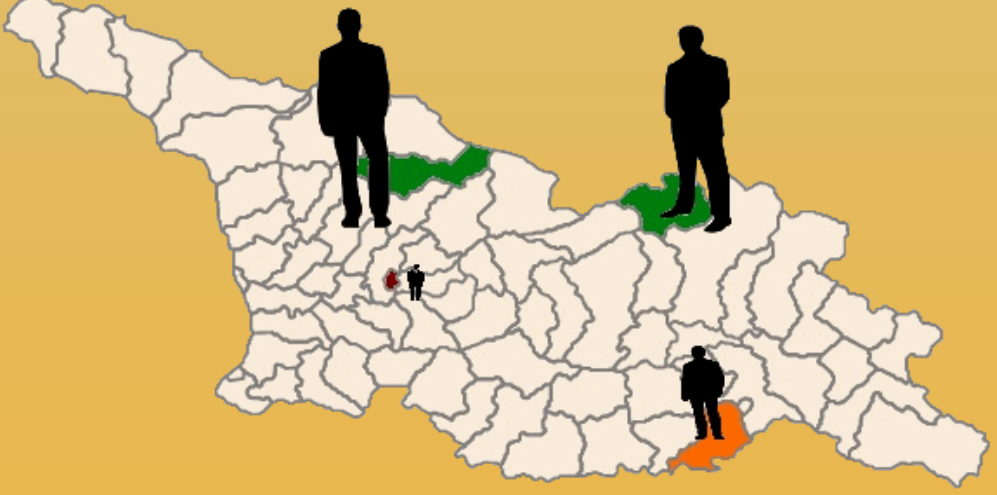But there is also a more obvious problem: when the districts to elect a single representative have widely different numbers of voters. However obvious a requirement equality is, see for instance the map of Georgia with the figures standing for the level of representation of different voting districts in 2010. Differences have been over 38-fold!

While such a difference is difficult to explain having perfectly equal districts is practically imposible. This is especially true when the borders must respect administrative or geographic borders. Apportionment is done very carefully in the United States, but voters in Rhode Island have some 88% more representation than those in Montana. 

Our paper was motivated by the new elections law of Hungary. The law was passed while Viktor Orbán had a two-third majority in the parliament, so it could be passed without the usual compromises: the hotbed for gerrimandering and all sorts of other manipulation. 

The law closely followed the recommendations of the Venice Commission, the European Commission for Democracy through Law: the districts must respect administrative boundaries and there is a maximum permitted difference from the average district size. In addition smaller towns cannot be split and districts must be connected. The design of districts has three steps

1. The apportionment of house seats among administrative regions.
2. Allocating smaller towns among districts
3. Drawing the fine lines in larger towns.

Steps 2 and 3 give room for gerrymandering, although this presumes that the legislators know the voters preferences, which in a country that went from 2/3 liberal-left majority to 2/3 conservative majority may not work too well. Step 2 is an interesting issue and is far from trivial if no large towns are around. We looked at Step 1 assuming that within counties the division of voters can be perfect.

 We propose the Leximin apportionment rule. Going beyond the recommendation of the VC we look for the apportionment with the smallest largest difference. In Hungary, for instance this means that Tolna should get 3 districts (a 15.28% difference based on 2010 data), but leaves a lot of freedom for the rest. We do not like such freedom leading to arbitrary (or arbitrary-looking) decisions so suggest to try to minimise the next largest difference, and so on. The result is not only attractive mathematically, but is unique up to symmetries. It turns out, by the way that the apportionment used in the law is nearly optimal (and we also think we can explain the difference).

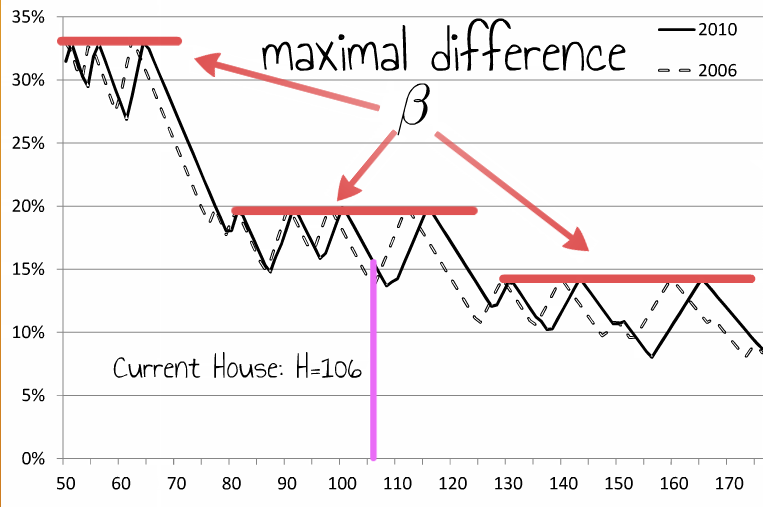
Given the method, we can also make some interesting observations. Is 15.28% difference too much? Actually this is one of the best scenarios we can get with these (voters') population sizes. With slightly less or more representatives the number could go up to 20%. In fact we would need about 130 districts (up from 106) to be sure to be under 15% as the figure below shows.

We have also looked at other countries. In Germany the smallest largest difference is nearly 17% due to Bremen. This cannot be improved upon, but if Mecklenburg-Vorpommern would get 7 instead of 6 districts, taking one away from Hesse, the second largest difference could be reduced to 6.86% from 8.66%. Transferring a seat from Baden-Württemberg to Bavaria would further improve the apportionment.

In the United States the apportionment of the seats of the House of Representatives is difficult as one has to allocate them among many regions: the states. It is therefore not so surprising that the largest difference is 39.9% at Montana, but this could be lowered to 30% by transferring one seat from California. 

Such a transfer is, however unlikely, as the apportionment method used in the US is the result of centuries of debates and compromises. It, for instance satisfies (house) monotonicity, that is, each state will get weakly more seats if the number of seats increases. This property is violated not only by the Leximin method, but by the largest difference property and thereby also by the recommendation of the Venice Commission - the conflict between equality and monotonicity is an interesting finding by itself. 

So one has to make a choice; the Venice Commission recommends equality and the the Leximin method gives a well-defined, easily computable apportionment. 

The paper:

Biró, P.; Kóczy L. Á.; Sziklai, B.  (2015): Fair apportionment in the view of the Venice Commission’s recommendation, Mathematical Social Sciences  77, 32-41.

or see the presentation below.